Length Of A Curve...

     aka Arclength

 

 

The most amazing and awesome part of calculus.

 

Have do we find the length of the curve of a graph of y=f(x)?

And how can we do it if the graph is constantly changing?

 

APPROXIMATIONS!!!!!!!

 

 

 

 

http://www.bbc.co.uk/schools/gcsebitesize/maths/images/graph_7.gif&imgrefurl=http://www.bbc.co.uk/schools/gcsebitesize/maths/algebra/graphsrev4.shtml&usg=__D1OEZjnCrH0wSdeTn5zo6MizKKc=&h=394&w=546&sz=12&hl=en&start=5&um=1&tbnid=uaN2HTQn0EEq2M:&tbnh=96&tbnw=133&prev=/images%3Fq%3Dy%253D3x%252B1%26um%3D1%26hl%3Den%26rlz%3D1T4GGLL_en%26sa%3DN

 

 

If we wanted to know the length of y=3x+1 from x=0 to x=1, we would use the PYTHAGOREAN THEOREM!!!

WOOHOO!!

 

so...

 

The base leg has a length of 1, and the other leg has a length of 3. Using the pythagorean theorem we do:

 

√((1)²+(3)²)= √(10)

 

The Length of f(x) from point (0,1) to point (1,4) is √(10)

 

 

With non-linear graphs,however, finding the arclength gets more difficult. With a curved graph you can't find the exact length using the pythagorean theorem as we used before. That's why we appoximate. Lets say we get the graph:

 

                         y=x²+5x

 

 

 

We have a non-linear graph. I personally want to know the length of the graph from point (0,0) to point (12,204). Because the pythagorean theorem worked so well before, we use it again, but as an approximation. For y= x² + 5x we use the integral. We take the integral from 0 to 12 of the square root of 1 + f'(x)². A generic formula would be

 

 

for our example we will plug in our numbers

  

 

= 204.4382639

 

The integral allows us to make a large amount of very very samll right triangles because the step size between two points are extremely small. We then use the hypotenuses of those small triangels to ≈ an arclength pretty accurately.

 

If we just did the normal pythagorean theorem we would get a much less accurate approximation.

 

 

Here we have just one triangle to approximate the length. One leg has a height of 204, and the other leg has a length of 12 so we do:

 

√((12²)+(204²))

 

 

to find the hypotenuse,which equals

204.353

 

Although these two values are  almost equal they are not the same. It mostly means I chose a bad example equation... hehe

So if the equation is not a straight line and you need the arclength use the formula!

 

 

 

 

pretty!!

 

 

 

 

 

Practice Problems

 

  

1) Find the arc length of the graph of 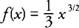on the interval [0,5]. 

http://www.cliffsnotes.com/WileyCDA/CliffsReviewTopic/Arc-Length.topicArticleId-39909,articleId-39908.html

 

 

 

 

 

 

 2) Find the arc length of the graph of f(x) = ln (sin x) on the interval [π/4, π/2]. 

http://www.cliffsnotes.com/WileyCDA/CliffsReviewTopic/Arc-Length.topicArticleId-39909,articleId-39908.html

 

 

 

3) Find the length of the graph  [3,10].

http://archives.math.utk.edu/visual.calculus/5/arclength.1/6.html 

 

 

 

4) What is the arc length of the curve of  y=ln(cosx)

A)

 

B)

C)

D)

E) 

F) 

 

  

 

 

5) Find the lentgth of 

http://blue.utb.edu/swyche/m2414a/cal_1_final_a/index.htm

 

A) 9/16

B) 335/432

C) 335/288

D) 335/3

 

6)Find the length of 

http://blue.utb.edu/swyche/m2414a/cal_1_final_a/index.htm

 

A) 9/4

B) 335/108

C) 335/288

D) 355/3

 

SOLUTIONS!.doc