Polar Equations:

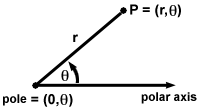
     in the cartesian plane, points are at (x,y) with x being horizontal displacement from the origin and y being the vertical displacement.  with polar equations, we use the coordinates (r,Θ) with r being the distance between the point and the pole and Θ being the angle betweent the polar axis and the ray containing the point whose endpoint is also the pole (see figure).

   to convert a regular equation to a polar equation, we use:

• x = rcosΘ

  y = rsinΘ

For circles;

the common circle, r=c where c is a constant. for a circle that intersects the pole once has the equation r=acosΘ or r=asinΘ where a is the diameter of the circle

For limacons;

r=a+bcosΘ or r=a+bsinΘ where a,b≠0

For petal curves;

r=a cos nΘ or r=a sin nΘ.  If n is a positive even integer, then the curve has 2n petals.  If n is a positive odd integer, the curve has n petals.  If n is not and integer, then the petals overlap. The length of the petals is a.

For spirals;

there are two common kinds of spirals;

    Archimides spiral which has the equation r=aΘ+b and

    logistic spiral which has the equation r=ab^Θ

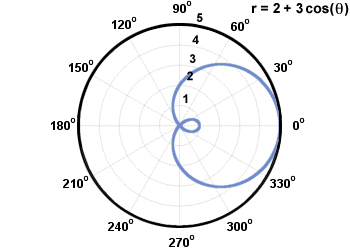
        Polar Rose                                                       Circle                                                                   Limacon

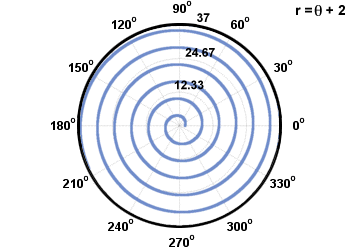
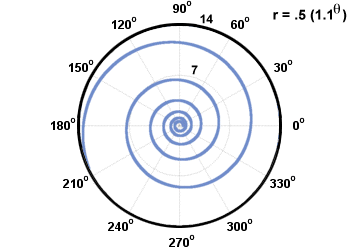
            Archimedes Spiral                                                                   Logistic Spiral

Problems:

1) Given a point in rectangular coordinates (x, y), express it in polar coordinates (r, θ) two different ways such that 0≤θ < 2π: (x, y) = (- 4, 0)

       a) (-4,π),  (4,0)

       b) (4,-π), (-4,0)

       c) (4,π), (-4,0)

       d) (-4,-π), (4,0)

2) Decide whether each of the following polar graphs is a limacon, a rose curve, a spiral, a circle, or none of these:

        a) r = 2 + cos(θ)

        b) r = 2

        c) r = sin(3θ)

        d) r = 1 - cos(θ)

        e) r = 2θ

3) Convert to rectangular form the circle, with the polar equation, R = 4sint

       a) x ² + y ² + 4 y = 0

       b) x ² + y ² - 4 y = 0

       c) x ² - y ² - 4 y = 0

       d) x ² - y ² + 4 y = 0

4) The area of the closed region bounded by the polar graph of r = 2 + 2cosθ is

       a) 4.712

       b) 9.424

       c) 18.849

       d) 37.699

         e) 75.398

5) Find the intercepts and zeros of the following polar equations:

        a) r = cos(θ) + 1

        b) r = 4 sin(θ)

 6) Consider the polar curve r = 2 sin(3θ) for 0≤θ≤π

        (a)    In the xy-plane provided below, sketch the curve.

        (b)    Find the area of the region inside the curve.

        (c)    Find the slope of the curve at the point where θ = π/4

Visual Aid:

http://www.analyzemath.com/polarcoordinates/polarcoordinates.html

http://www.ies.co.jp/math/java/calc/sg_kyok/sg_kyok.html

Sources:

http://ltcconline.net/greenl/courses/107/PolarParam/POLAR.HTM

http://www.sparknotes.com/math/precalc/parametricequationsandpolarcoordinates/section2.rhtml

http://www.sparknotes.com/math/precalc/parametricequationsandpolarcoordinates/section3.rhtml

http://en.wikipedia.org/wiki/Polar_coordinates

http://jwilson.coe.uga.edu/EMT668/EMAT6680.2003.fall/Ramachandran/Assignments/Asmt11/assingment_11/assignment_11.htm

Solutions:

1) C

2) limacon; circle; rose curve; limacon; spiral

3) B

4) C

5) (2, 2nπ), (0,(2n + 1)π), where n is an integer; (0, nπ) where n is an integer

6)

; A=π; dy/dx = 1/2

For additional problems, go to:

http://education.yahoo.com/homework_help/math_help/problem_list?id=miniprecalcgt_7_1